Edit

Acquisition Functions

Acquisition functions are heuristics employed to evaluate the usefulness of one of more design points for achieving the objective of maximizing the underlying black box function.

BoTorch supports both analytic as well as (quasi-) Monte-Carlo based acquisition functions. It provides a generic AcquisitionFunction API that abstracts away from the particular type, so that optimization can be performed on the same objects.

Monte Carlo Acquisition Functions

Many common acquisition functions can be expressed as the expectation of some real-valued function of the model output(s) at the design point(s):

$$ \alpha(X) = \mathbb{E}\bigl[ a(\xi) \mid \xi \sim \mathbb{P}(f(X) \mid \mathcal{D}) \bigr] $$

where $X = (x_1, \dotsc, x_q)$, and $\mathbb{P}(f(X) \mid \mathcal{D})$ is the posterior distribution of the function $f$ at $X$ given the data $\mathcal{D}$ observed so far.

Evaluating the acquisition function thus requires evaluating an integral over the posterior distribution. In most cases, this is analytically intractable. In particular, analytic expressions generally do not exist for batch acquisition functions that consider multiple design points jointly (i.e. $q > 1$).

An alternative is to use Monte-Carlo (MC) sampling to approximate the integrals. An MC approximation of $\alpha$ at $X$ using $N$ MC samples is

$$ \alpha(X) \approx \frac{1}{N} \sum_{i=1}^N a(\xi_{i}) $$

where $\xi_i \sim \mathbb{P}(f(X) \mid \mathcal{D})$.

For instance, for q-Expected Improvement (qEI), we have:

$$ \text{qEI}(X) \approx \frac{1}{N} \sum_{i=1}^N \max_{j=1,..., q} \bigl\{ \max(\xi_{ij} - f^*, 0) \bigr\}, \qquad \xi_{i} \sim \mathbb{P}(f(X) \mid \mathcal{D}) $$

where $f^*$ is the best function value observed so far (assuming noiseless observations). Using the reparameterization trick (^[1], ^[2]),

$$ \text{qEI}(X) \approx \frac{1}{N} \sum_{i=1}^N \max_{j=1,..., q} \bigl\{ \max\bigl( \mu(X)_j + (L(X) \epsilon_i)_j - f^*, 0 \bigr) \bigr\}, \qquad \epsilon_{i} \sim \mathcal{N}(0, I) $$

where $\mu(X)$ is the posterior mean of $f$ at $X$, and $L(X)L(X)^T = \Sigma(X)$ is a root decomposition of the posterior covariance matrix.

All MC-based acquisition functions in BoTorch are derived from MCAcquisitionFunction.

Acquisition functions expect input tensors $X$ of shape $\textit{batch_shape} \times q \times d$, where $d$ is the dimension of the feature space, $q$ is the number of points considered jointly, and $\textit{batch_shape}$ is the batch-shape of the input tensor. The output $\alpha(X)$ will have shape $\textit{batch_shape}$, with each element corresponding to the respective $q \times d$ batch tensor in the input $X$. Note that for analytic acquisition functions, it must be that $q=1$.

MC, q-MC, and Fixed Base Samples

BoTorch relies on the re-parameterization trick and (quasi)-Monte-Carlo sampling for optimization and estimation of the batch acquisition functions ^[3]. The results below show the reduced variance when estimating an expected improvement (EI) acquisition function using base samples obtained via quasi-MC sampling versus standard MC sampling.

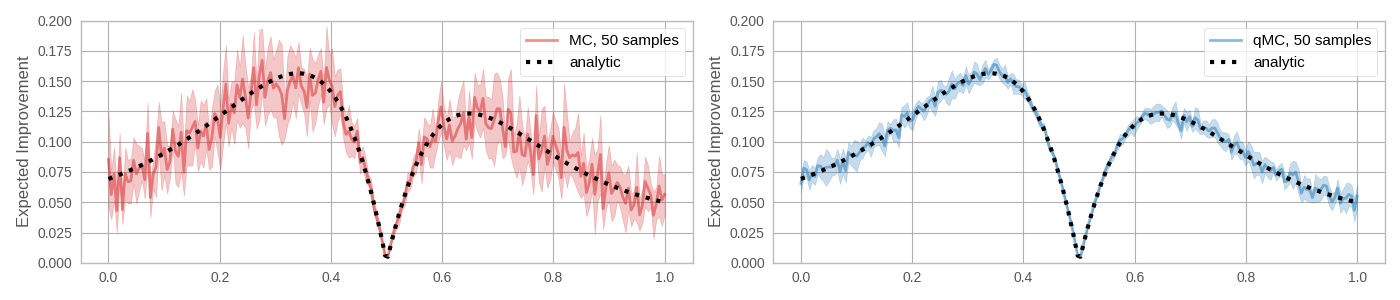
In the plots above, the base samples used to estimate each point are resampled. As discussed in the Overview, a single set of base samples can be used for optimization when the re-parameterization trick is employed. What are the trade-offs between using a fixed set of base samples versus re-sampling on every MC evaluation of the acquisition function? Below, we show that fixing base samples produces functions that are potentially much easier to optimize, without resorting to stochastic optimization methods.

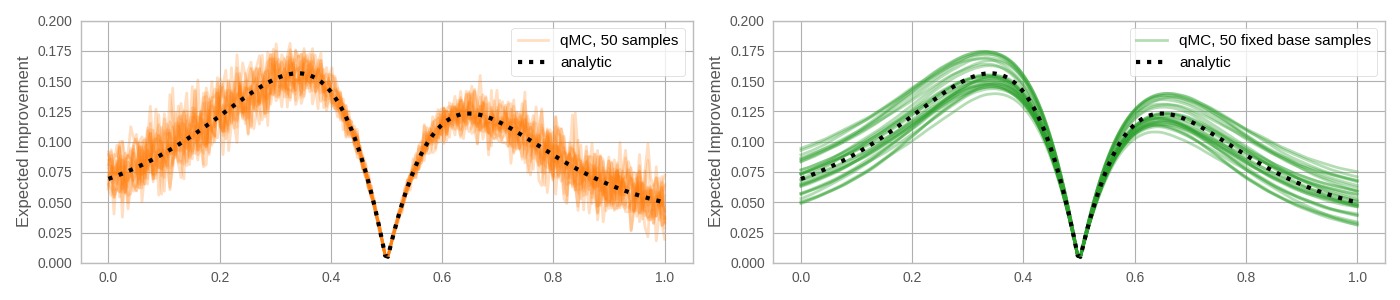
If the base samples are fixed, the problem of optimizing the acquisition function is deterministic, allowing for conventional quasi-second order methods such as L-BFGS or sequential least-squares programming (SLSQP) to be used. These have faster convergence rates than first-order methods and can speed up acquisition function optimization significantly.

One concern is that the approximated acquisition function is biased for any fixed set of base samples, which may adversely affect the solution. However, we find that in practice, both the optimal value and the optimal solution of these biased problems for standard acquisition functions converge quite rapidly to their true counterparts as more samples are used. Note that for evaluation of the acquisition function we integrate over a $qo$-dimensional space (where $q$ is the number of points in the q-batch and $o$ is the number of outputs included in the objective). Therefore, the MC integration problem can be quite low-dimensional even for models on high-dimensional feature spaces (large $d$). Because using additional samples is relatively cheap computationally, we default to 500 base samples in the MC acquisition functions.

On the other hand, when re-sampling is used in conjunction with a stochastic optimization algorithm, the kind of bias noted above is no longer a concern. The trade-off here is that the optimization may be less effective, as discussed above.

Analytic Acquisition Functions

BoTorch also provides implementations of analytic acquisition functions that do not depend on MC sampling. These acquisition functions are subclasses of AnalyticAcquisitionFunction and only exist for the case of a single candidate point ($q = 1$). These include classical acquisition functions such as Expected Improvement (EI), Upper Confidence Bound (UCB), and Probability of Improvement (PI). An example comparing ExpectedImprovement, the analytic version of EI, to it's MC counterpart qExpectedImprovement can be found in this tutorial.

Analytic acquisition functions allow for an explicit expression in terms of the summary statistics of the posterior distribution at the evaluated point(s). A popular acquisition function is Expected Improvement of a single point for a Gaussian posterior, given by

$$ \text{EI}(x) = \mathbb{E}\bigl[ \max(y - f^*, 0) \mid y\sim \mathcal{N}(\mu(x), \sigma^2(x)) \bigr] $$

where $\mu(x)$ and $\sigma(x)$ are the posterior mean and variance of $f$ at the point $x$, and $f^*$ is again the best function value observed so far (assuming noiseless observations). It can be shown that

$$ \text{EI}(x) = \sigma(x) \bigl( z \Phi(z) + \varphi(z) \bigr)$$

where $z = \frac{\mu(x) - f_{\max}}{\sigma(x)}$ and $\Phi$ and $\varphi$ are the cdf and pdf of the standard normal distribution, respectively.

With some additional work, it is also possible to express the gradient of the Expected Improvement with respect to the design $x$. Classic Bayesian Optimization software will implement this gradient function explicitly, so that it can be used for numerically optimizing the acquisition function.

BoTorch, in contrast, harnesses PyTorch's automatic differentiation feature ("autograd") in order to obtain gradients of acquisition functions. This makes implementing new acquisition functions much less cumbersome, as it does not require to analytically derive gradients. All that is required is that the operations performed in the acquisition function computation allow for the back-propagation of gradient information through the posterior and the model.

---

1. D. P. Kingma, M. Welling. Auto-Encoding Variational Bayes. ICLR, 2013. ↩

2. D. J. Rezende, S. Mohamed, D. Wierstra. Stochastic Backpropagation and Approximate Inference in Deep Generative Models. ICML, 2014. ↩

3. J. T. Wilson, R. Moriconi, F. Hutter, M. P. Deisenroth. The Reparameterization Trick for Acquisition Functions. NeurIPS Workshop on Bayesian Optimization, 2017. ↩